首先要聲明一下,這篇文章不是要解答或表示個人想法或觀點。
反而是希望透過集結各路菁英的網路也順便幫我解惑
網友 pda 提出了以下的問題:
忠孝兄您好,我想請問您有關於股息折現公式的問題,就是透過股息折現公式計算出來的報酬率,有包含每年股息的再投入嗎(就是以每年的股息都有再進場買股票為前提計算出的報酬率)? 還是晾在一旁沒有投入呢? 有人認為沒有,不過就公式看起來我覺得應該是有才對,所以特來請教您一下。謝謝~ ^^
前一陣子在巴菲特班的討論中,這可是一個極度熱門的話題,不過在各方正反兩方各擁證據下,這問題似乎沒有一個明確的解答。說實在的,我個人對於估值僅限於應用階段,原理當然還是會試圖瞭解,但是像標題這麼深入的問題,我還真沒仔細用心思考過,主要是本著巴菲特說:「寧願模糊的對也不要精確的錯」,所以過去對這樣的問題就不是很介意了。
不過既然有網友提出,我還是很好奇地想辦法驗證一下。因此透過 Excel 來試著尋求答案: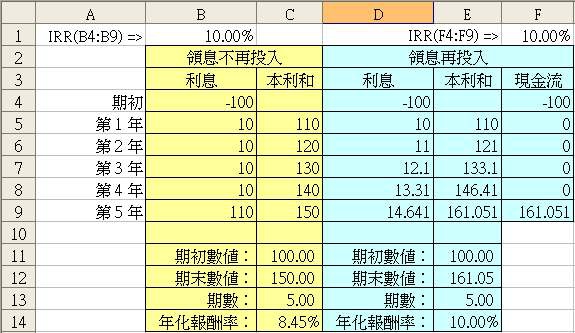
上圖中 B1 的公式已經顯示於 A1 中,計算期初付出一百元後,往後每年都可以領到 十元的配息,五年期滿後連同本金領回 110,IRR 函數計算這個投資的內部報酬率為 10%。很明顯地,這屬於領息不再投入(單利)的投資,而右邊則同樣是以 10% 的利率且每年還將10%的利息收入再投入的投資(複利),第五年後領回 161.051 元。
有意思的是,左邊領息不再投入的投資,計算年化報酬時卻只有 8.45%,而右邊領息再投入的年化報酬率確切的答案正好是 10%。所以 IRR 有隱含再投入的意思嗎?從上面這例子來看,似乎並沒有。
但是!!!在我尋尋覓覓答案的過程中,皇天不負苦心人讓我從這個部落格(brandonkhlin / NPV IRR MIRR)看到下面這一段:
|
也可以用另一個角度看這IRR,用最簡單的報酬率觀念來檢視,就是假設只有兩筆現金流量,一個是期初投入(PV),另一個是以利率R經過n期後的期末淨值(FV) 因為FV = PV*(1 + R)n R = (FV/PV)1/n -1 -----------(3) 在上面例子裡n等於5年,PV是100萬。然後將期中每年分批之現金流入以IRR (21.14%)成長到第5年,期末淨值FV: 套上式子(3),年化報酬率R =(2608802/1000000)^(1/5) - 1 = 21.14% 上面的結論顯示:內部報酬率隱含著每年分批進來的現金流入(收入),都以IRR的利率成長至期末,所換算回來的年化投資報酬率。 |
該篇解釋 NPV、IRR、MIRR 的說明挺清楚的,而且還一步步演算,立論也很明瞭,何況既然有 MIRR 的出現,正說明 IRR 有其不切實際之處。
只是我就很難理解何以我上面所設定領息不再投入的例子怎麼會有 B1 跟 C14 的差異呢?原因為何? 還請更聰明的網友大眾們給予指教,不吝感激!
2010/07/20
經由網友 IcySwordRain 的提醒,我在原來的範例圖檔中新增 F 欄的情況。由於 IRR 是未來預期現金流量的折現,所以若將原先應該領到的股息收入再投入,那當期的現金流應該為零。而如此在 F1 計算得到的 IRR 的確也是 10%。從這樣的結果我們的確可以歸納出 IRR 本身的計算果然隱含著股息再投入的意涵。
網友 Leon Chen 所引述的資料也提到單純用 IRR 來做投資決策可能遇到的問題。



 留言列表
留言列表
